無リスク金利上昇によるPERの変化

前回の記事ではNYダウ構成銘柄の現在のPERと、PERに織り込まれている成長率を計算しました。
（過去記事：NYダウ構成銘柄のPERと織り込まれている成長率）

前回は無リスク金利（米10年国債利回り）＝2.12％として計算しましたが、米10年国債利回りは昨年10月には3.26％まで上昇しました。

今後も金利低下が続くのか底打ちするのかは分かりませんが、低下余地よりは上昇余地のほうが大きそうに思えます。

個人的には2.12％という低金利を前提に考えるのは株式にとって有利すぎるように感じるので、今回は金利が上昇していったらどうなるのかを考えてみました。

無リスク金利上昇によるPERの変化

成長率を一定とした場合

まずは成長率を一定とした場合です。

現在の株式リスクプレミアムが5.96％、無リスク金利が2.12％とすると、成長率ごとのPERは以下のようになります。
（PER ＝1/（無リスク金利＋株式リスクプレミアム－成長率））

成長率	PER
-10%	5.53
-9%	5.85
-8%	6.22
-7%	6.63
-6%	7.10
-5%	7.65
-4%	8.28
-3%	9.03
-2%	9.92
-1%	11.01
0%	12.38
1%	14.12
2%	16.45
3%	19.69
4%	24.51
5%	32.47
6%	48.08
7%	92.59
8%	1,250.00

無リスク金利が現在の2.12％から2.5％、3.0％、3.5％、4％と上昇していった場合、PERは以下のように変化します。
（この場合、成長率が高すぎると分母がほぼゼロになってPERは無限大になってしまうため、成長率が割引率を上回るところは「-」になっています。）

成長率	無リスク金利
	2.12%	2.50%	3.00%	3.50%	4.00%
-10%	5.53	5.42	5.27	5.14	5.01
-9%	5.85	5.73	5.57	5.42	5.27
-8%	6.22	6.08	5.90	5.73	5.57
-7%	6.63	6.47	6.27	6.08	5.90
-6%	7.10	6.92	6.68	6.47	6.27
-5%	7.65	7.43	7.16	6.92	6.68
-4%	8.28	8.03	7.72	7.43	7.16
-3%	9.03	8.73	8.36	8.03	7.72
-2%	9.92	9.56	9.12	8.73	8.36
-1%	11.01	10.57	10.04	9.56	9.12
0%	12.38	11.82	11.16	10.57	10.04
1%	14.12	13.40	12.56	11.82	11.16
2%	16.45	15.48	14.37	13.40	12.56
3%	19.69	18.32	16.78	15.48	14.37
4%	24.51	22.42	20.16	18.32	16.78
5%	32.47	28.90	25.25	22.42	20.16
6%	48.08	40.65	33.78	28.90	25.25
7%	92.59	68.49	51.02	40.65	33.78
8%	1,250.00	217.39	104.17	68.49	51.02
9%	-	-	-	217.39	104.17
10%	-	-	-	-	-

たとえば無リスク金利2.12％で織り込まれている成長率が0％ではPERは12.38になりますが、無リスク金利が2.50%に上昇すると11.82、3.00％では11.16、3.50％では10.57、4.00％では10.04となります。

PER変化率は無リスク金利2.12％→2.50％では-4.5％、2.12％→3.00％では-9.8％、2.12％→3.50％では-14.6％、2.12％→4.00％では-18.9％です。

一方、無リスク金利2.12％で織り込まれている成長率が5％の場合、PERは32.47になりますが、無リスク金利が2.50%に上昇すると28.90、3.00％では25.25、3.50％では22.42、4.00％では20.16となります。

この場合、PER変化率は無リスク金利2.12％→2.50％では-11.0％、2.12％→3.00％では-22.2％、2.12％→3.50％では-30.9％、2.12％→4.00％では-37.9％です。
 
このように、無リスク金利上昇によるPER縮小率は高PER株（織り込まれている成長率が高い）ほど大きく、低PER（織り込まれている成長率が低い）ほど小さくなります。

上表をグラフ化すると以下のようになります。

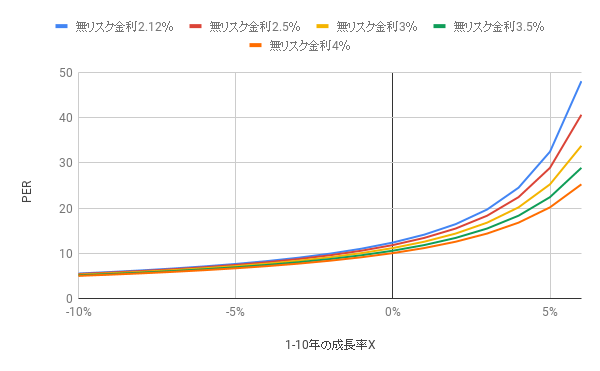
1-10年目の成長率＝X％、11年目以降＝4％とした場合

前回と同様、1-10年目の成長率＝X％、11年目以降＝2％（インフレ率並み）としたとき、PERは以下のようになります。

成長率X	PER
-10%	6.87
-9%	7.38
-8%	7.93
-7%	8.53
-6%	9.18
-5%	9.88
-4%	10.65
-3%	11.47
-2%	12.37
-1%	13.35
0%	14.40
1%	15.54
2%	16.78
3%	18.11
4%	19.56
5%	21.12
6%	22.81
7%	24.64
8%	26.61
9%	28.74
10%	31.04
11%	33.51
12%	36.18
13%	39.06
14%	42.16
15%	45.50
16%	49.09
17%	52.95
18%	57.10
19%	61.56
20%	66.35

無リスク金利が現在の2.12％から2.5％、3.0％、3.5％、4％と上昇していった場合、PERは以下のように変化します。

成長率X	無リスク金利
	2.12%	2.50%	3.00%	3.50%	4.00%
-10%	6.87	6.56	6.21	5.90	5.63
-9%	7.38	7.04	6.65	6.31	6.01
-8%	7.93	7.56	7.12	6.75	6.42
-7%	8.53	8.12	7.64	7.22	6.86
-6%	9.18	8.72	8.20	7.74	7.33
-5%	9.88	9.38	8.80	8.29	7.85
-4%	10.65	10.09	9.45	8.89	8.40
-3%	11.47	10.86	10.16	9.54	9.01
-2%	12.37	11.70	10.92	10.25	9.65
-1%	13.35	12.60	11.75	11.01	10.36
0%	14.40	13.58	12.64	11.83	11.11
1%	15.54	14.64	13.61	12.71	11.93
2%	16.78	15.79	14.66	13.67	12.81
3%	18.11	17.03	15.79	14.71	13.77
4%	19.56	18.37	17.01	15.83	14.79
5%	21.12	19.82	18.32	17.03	15.90
6%	22.81	21.39	19.75	18.33	17.10
7%	24.64	23.08	21.28	19.74	18.39
8%	26.61	24.90	22.94	21.25	19.78
9%	28.74	26.87	24.73	22.88	21.27
10%	31.04	29.00	26.66	24.64	22.88
11%	33.51	31.29	28.73	26.53	24.61
12%	36.18	33.75	30.97	28.57	26.48
13%	39.06	36.41	33.38	30.76	28.49
14%	42.16	39.27	35.97	33.12	30.64
15%	45.50	42.35	38.75	35.65	32.96
16%	49.09	45.66	41.75	38.38	35.45
17%	52.95	49.23	44.97	41.31	38.13
18%	57.10	53.05	48.43	44.45	41.00
19%	61.56	57.17	52.15	47.83	44.08
20%	66.35	61.58	56.13	51.45	47.38

たとえば無リスク金利2.12％で織り込まれている成長率Xが0％ではPERは14.40になりますが、無リスク金利が2.50%に上昇すると13.58、3.00％では12.64、3.50％では11.83、4.00％では11.11となります。

PER変化率は無リスク金利2.12％→2.50％では-5.7％、2.12％→3.00％では-12.2％、2.12％→3.50％では-17.9％、2.12％→4.00％では-22.8％です。

一方、無リスク金利2.12％で織り込まれている成長率Xが10％の場合、PERは31.04になりますが、無リスク金利が2.50%に上昇すると29.00、3.00％では26.66、3.50％では24.64、4.00％では22.88となります。

この場合、PER変化率は無リスク金利2.12％→2.50％では-6.6％、2.12％→3.00％では-14.1％、2.12％→3.50％では-20.6％、2.12％→4.00％では-26.3％です。

こちらは11年目以降の成長をインフレ率並みの2％と低めに見積もっているので、先ほどの成長率を一定とした場合に比べると差が小さいです。

上表をグラフ化すると以下のようになります。

バイロン・ウィーンの配当割引モデル

フィナンシャル・ポインターで紹介されていたバイロン・ウィーンの配当割引モデルの早見表では、米10年国債利回りが2.0％→2.5％に上昇するとS&P500は22.7％、2.0％→3.0％に上昇すると37.0％下落するとなっています。

フィナンシャル・ポインターで紹介されてたバイロン・ウィーンの配当割引モデルの早見表。
現在はS&P500のEPSが166、米10年国債利回りが2％なので早見表では3,301になるとのこと。
ただし10年国債利回りが2.5％まで上昇すると2,551まで下落。
3％なら2,078、3.25％なら1,902。 pic.twitter.com/0QWVHguv6m

— 高卒非正規が株式投資でアーリーリタイアを目指す (@ronaldread_blog) July 13, 2019

こちらは金利感応度がかなり大きめですね。

まとめ

条件によって金利感応度は大きく違ってきますが、金利が上昇することでPERは縮小し、縮小率はPERが高くなるほど大きくなるのは同じです。

債券でも残存期間が長くなるほど金利感応度が高くなりますが、株式も同様にPERが高いほど金利の影響を受けやすく、PERが低いほど金利の影響を受けにくくなります。

少し前に読んだ記事で「グロース株は最もデュレーション※が長い資産だ」という記述があったのですが、まさにその通りですね。
 ※デュレーションとは金利変動に対してどれだけ債券価格が変動するかを表したものです。債券価格の変動率＝-（金利変動×デュレーション）で計算できるので、たとえばデュレーションが2年の債券は金利が1％上昇すると債券価格は2％下落します。


過去の長期金利上昇局面を調べてみると、どの期間もPERが縮小することで金利低下局面と比べて非常に低いリターンにとどまっています。
（過去記事：長期金利上昇局面と低下局面における米国株のリターン）
（過去記事：長期金利上昇局面ではバリュエーションが縮小する）

上記の記事を書いた時点では再び2％近くまで10年国債利回りが下がるとは全然思っていなかったですし、まだしばらくは上がらないのかもしれません。

でも永久に金利低下が続くことはないでしょうし、やがて資産価格にとって逆風の金利上昇局面がやってくる覚悟をもっておきたいと思っています。


よろしければ応援クリックお願いします